用R来进行布丰投针实验

在3月14日也就圆周率日那一天，果壳网推出一篇文章《圆周率日特献：π究竟牛B在哪里？》。其中就提到了布丰（Buffon）用投针实验来计算π的近似值。不过这篇文章并没有详细说明如何用软件来做这个实验，也看到网上有朋友在问具体的过程。所以本文尝试用R来实现这个实验，算是狗尾续貂以作消遣。另外，Maxtrix67和魏太云都对这个问题有过精彩的论述，有兴趣的朋友可以参考一下。

简单来讲，投针实验是指假设有两根平行的线，它们之间的距离是1。随意抛掷一根长度为0.5的针，那么投针便有机会与平行线相交。如果总的投掷次数为N，发生相交的次数为X，那么可以用N/X来估计π的值。具体的故事和公式还可以参考这个文章。

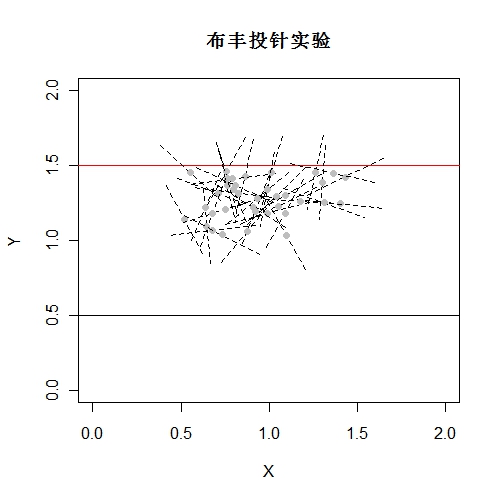
为了在R中实现这个实验过程，我们先绘制出一个空的图形，再加两根平行线。可以只考虑针与一条线的相交情况，我们用一个while循环来进行反复投针，其中用随机数来模拟投针的坐标和角度，并绘制在图形中。如果发现相交则增加变量cross的计数，同时用cat函数显示实验次数和估计值。下图是根据上述假设编写代码所绘制的图形。如果你自己在R语言中运行代码，可以按空格来反复投针，用y来结束实验，可以观察到当试验次数增加，估计值也随之接近真值。

R代码如下：
rm(list=ls())

# 绘制空白图形
plot(c(0,2),c(0,2),type='n',main='布丰投针实验',xlab='X',ylab='Y')
# 增加平行线
abline(h=0.5)
abline(h=1.5,col='red')
finished <- FALSE
# trial为实验次数，cross为交叉次数
trial <- 0
cross <- 0
while (!finished) {
    # Dist为针的中心距离红线的垂直距离
    # Theta为针的角度
    Dist <- runif(1,min=0,max=1/2)
    Theta <- runif(1,0,pi)
    # central.x为针中心点的横坐标
    # central.y为针中心点的纵坐标
    central.x <- runif(1,0.5,1.5)
    central.y <- Dist +1
    # 计算针两端的坐标
    y1 <- sin(Theta)/4 + central.y
    x1 <- cos(Theta)/4 + central.x
    y2 <- sin(Theta+pi)/4 + central.y
    x2 <- cos(Theta+pi)/4 + central.x
    trial <- trial +1
    # 计数交叉次数
    cross <- cross + ifelse(0.25*sin(Theta)>=Dist,1,0)
    # 绘制针的线型和中心点
    lines(c(x1,x2),c(y1,y2),lty=2)
    points(central.x,central.y,pch=16,col='grey')
    cat('trial=',trial,'cross=',cross,'PI=',trial/cross,'\n')
    #continue?
    input <- readline('stop?')
    # 若输入y，则结束实验
    if (input =='y') finished <- TRUE
}