需要几次相亲才能找到靠谱的她/他？

谈到相亲就不得不提到著名的麦穗问题。说有一天，苏格拉底带领几个弟子来到一块成熟的麦地边。他对弟子们说：“你们去麦地里摘一个最大的麦穗，但要求只能摘一次，只许进不许退，我在麦地的尽头等你们。”可以看得出，相亲这种活动就有点类似于摘麦穗，在等待和决断之间达成平衡是解决问题的重点。

将上述的麦穗问题进一步抽象就是一个经典的概率问题。若一个袋子里有100个不同的球。每个球上标明了其尺寸大小。我们每次随机无放回的从袋中取一个球出来，观察其大小属性之后需决定要或是不要。如果要，取球就此停止。如果不要， 再继续取球，但不准再回头要原先的球。这样下去，直到100个球取完为止。目的就是取到那个最大的球。

对于这个概率问题，一种思路就是取1到100之间的某个数字n，以它作为分割点将整袋球划分为两组，第一组即从第1个到第n个球，第二组即从第n+1个到第100个球。我们以第一组为观察对象，找到第一组中最大的球M，记录其大小但并不行动。然后从第二组中寻找大于M的第一个球，选取该球。那么n应该设为多少，才能使取到最大球的概率最高呢？Ross在其《概率论基础教程》中已经给出了解析解，n应该取在1/e，也就是所有数目的37%处。

换句话说，如果你确定在生命中会遇到100个对象，那么对前37个就请按捺住你的热情，判定其中最优秀的那位M，然后再去寻找比M更优秀的，如果真的遇到就立刻行动，不要再犹豫。因为她/他很可能就是Mr. Right。

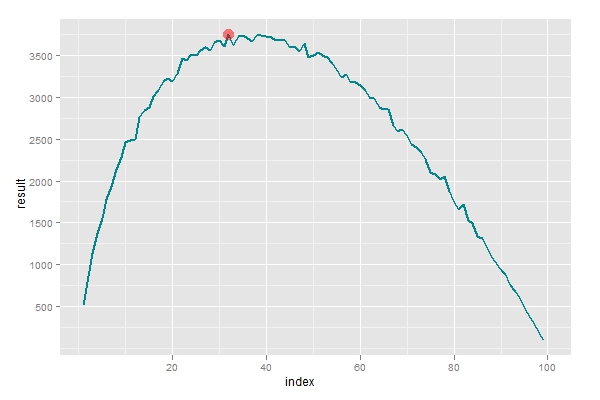
口说无凭，我们用R来检测一下上面的结论。先构造一个用于选择的函数，输入参数n是数据的分割点，输出即为选取得到的结果，如果得到100表明选取得到最优秀的对象，如果得到0则表明一无所获。然后设置n取值范围从1到100，对每个n的值模拟10000次选取行为，计算出给定n条件下得到最大值的概率。从下图可以看到最大值的确取在37附近，符合理论结果。

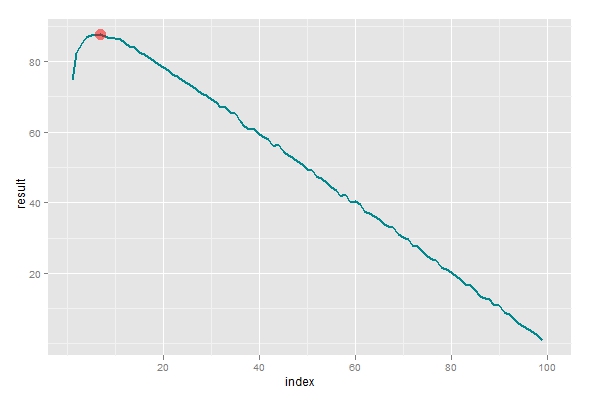
但这里还有一个问题，最优解不一定是令人满意的。如果我们以37作为分割点，可以计算出，有36%的可能性会得到最优的对象，但也有接近38%的可能会一无所获。实际上，有时候我们宁可得到一个次优的结果（例如99）也不希望孤独的生活。所以在选择n这个参数的时候，目标应该着重于结果的期望值大小。重新编程进行第二次模拟，从下图可以观察到最优值取在7附近。也就是说，如果你确定在生命中会遇到100个对象，那么前7个就略过，判定其中最优秀的那位M，然后再去寻找比M更优秀的，这样有最大的可能得到靠谱的对象。

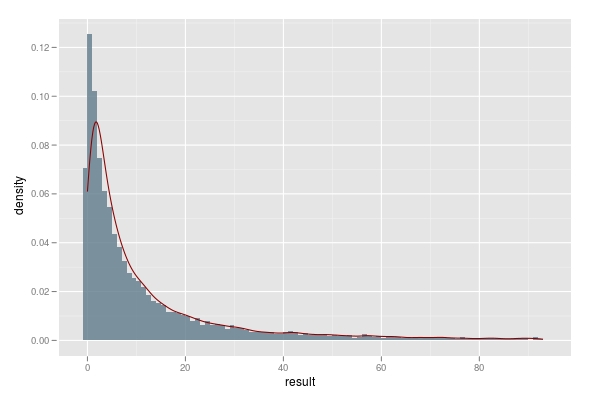
好了，我们知道了应该在观察7个对象后就开始行动，那么回到本文的题目上来，也就是需要多少次相亲才能碰上Mr. Right呢？我们先构造一个函数来记录在第二组中进行尝试的次数。然后模拟10000次后绘制直方图如下，可以看到仍然有7%左右的人未能找到合适的对象，而50%的人在10次以内的尝试后即能选取到合适的对象（未加上第一组的7次观察活动），80%的人在30次以内尝试后即能找到合适的对象。所以说，只要你人品不是太差，37次相亲应该就可以找到不错的人了。准备好你的时间和money吧，但愿你不会掉到离群点中去。

注：本文亦同时发布到统计之都上。本文结论有很多隐藏前提，其推理亦可能有失误之处，仅供娱乐。若读者完全以本文为指导进行相亲活动，其后果概不负责。^_^

R代码如下：
# 进行观察和选取的函数，n负责对整体进行划分，取值在1到100之间

selection <- function(n) {
  raw.data <- sample(1:100,100)
  first.group <- raw.data[1:n]
  second.group <- raw.data[(n+1):100]
  first.max <- max(first.group)
  morethan.first <- second.group > first.max
  my.select <- ifelse(any(morethan.first) == TRUE, 
                      second.group[morethan.first][1],0)
  return(my.select)
}
 
# 进行第一次模拟，找到最优的划分参数，使选取到最大值的概率最大。
data <- matrix(rep(0,10000*100),ncol=100)
result1 <- rep(0,100)
for (i in 1:100) {
  temp <- replicate(n=10000,selection(i))
  data[ ,i] <- temp
  result1[i] <- sum(data[,i] == 100)
}
which.max(result1)
 
# 用ggplot2绘图包进行观察
library(ggplot2)
index <- 1:100
p <- ggplot(data=data.frame(index,result1),aes(index,result1))
p+geom_line(size=1, colour='turquoise4') + 
  geom_point(aes(x = which.max(result1),y=result1[which.max(result1)]),colour=alpha('red',0.5),size=5) 
 
 
# 进行第二次模拟，找到最优的划分参数，使选取的期望值达到最大
result2 <- rep(0,100)
for (i in 1:100) {
  result2[i] <- mean(replicate(n=10000,selection(i)))
}
p <- ggplot(data=data.frame(index,result2),aes(index,result2))
p+geom_line(size=1, colour='turquoise4') + 
  geom_point(aes(x = which.max(result2),y=result2[which.max(result2)]),colour=alpha('red',0.5),size=5)
 
# 构造函数，记录需要多少次尝试才能选取较优的对象
howmany <- function(n) {
  raw.data <- sample(1:100,100)
  first.group <- raw.data[1:n]
  second.group <- raw.data[(n+1):100]
  first.max <- max(first.group)
  morethan.first <- second.group > first.max
  which.select <- ifelse(any(morethan.first) == TRUE, 
                      which(morethan.first==T)[1],0)
  return(which.select)
} 
 
# 记录尝试次数的10000次模拟结果，并绘制直方图
result3<- replicate(n=10000,howmany(7))
p <- ggplot(data=data.frame(result3),aes(result3))
p + geom_histogram(binwidth=1, position='identity',
    alpha=0.5,fill='lightskyblue4',aes(y = ..density..,))+
    stat_density(geom = 'line',colour='red4')
 
# 观察10次尝试内可选取到合适对象的人数比例
length(result[result>0 & result <10])/10000
length(result[result>0 & result <30])/10000