如何用21点来击败赌场？

21点也许是世界上最受欢迎的扑克牌游戏之一。玩家要尽量使手中牌的点数和达到21点，或是接近21点，但不能超过，再和庄家比较点数和的大小以定输赢。熟悉概率的诸位都知道，在赌场的各类游戏中，庄家有着绝对的优势。但二十一点却是唯一有机会击败庄家的游戏，也是最需要冷静和计算的游戏。其秘诀就在于记牌和算牌，即玩家要记住所有打出去的牌，然后再决定如何打剩下的牌。

为什么记牌能够有用，其原因在于条件概率。假设赌场使用一副牌来玩21点，庄家发出牌来，你拿到两个10（包括了J、Q、K），庄家亮牌也是10，翻出底牌来还是10，那么下一轮里10出现的概率已不再是4/13，而是12/48，即1/4，略低于4/13。所以在21点的各轮之间（在重新洗牌之前），出现10点的概率不再是独立的。前一轮出现过的牌，会影响到下一轮。因此，如果我们能记住前面出过什么牌，就能大致预测以后的赌局，从而占到一定的优势。

那么前面出现什么样的牌会对玩家有优势呢？答案是小牌。如果在前面10以下的小牌出现很多，意味着在剩下的牌局中，10出现的概率增大。而10点这种大牌对庄家是不利的。因为赌场规定了，庄家在16点及更低时必须要牌，10越多，就越容易使庄家爆掉。而对玩家来说，只需要在12点及以下时要牌。因此，玩家的优势就在于可以选择是否加入牌局。若观察到某个牌桌上已经出现了大量的小牌，就可以加入赌局，等待庄家爆牌送钱。

UCLA的数学教授爱德华·索普（Edward Thorp）在六十年代初发明了正式的21点算牌法。那时计算机也发明出来了，他找到IBM公司里的朋友，写了个程序来验证自己的算牌方法。那时的计算机足足运转了七天七夜，终于证明了这个方法是可行的。索普又自己到赌场里亲自实践，果然大赢特赢。1962年他出版了《打败庄家（Beat the Dealer）》一书，向公众介绍了自己的算牌法。《打败庄家》在刚出版时轰动一时，很快成为畅销书，激励了无数赌徒涌向赌场。赌场对此大为恐慌，有些甚至关闭了二十一点赌桌。但是，很快他们发现，只有极少数人真正掌握了算牌法，其他大多数人只不过是一知半解、道听途说。索普本人在60年代后期就淡出了赌博界，带着他在赌场赢来的大笔资金，进入股票市场，运用他的数学知识，现在已成为超级巨富。

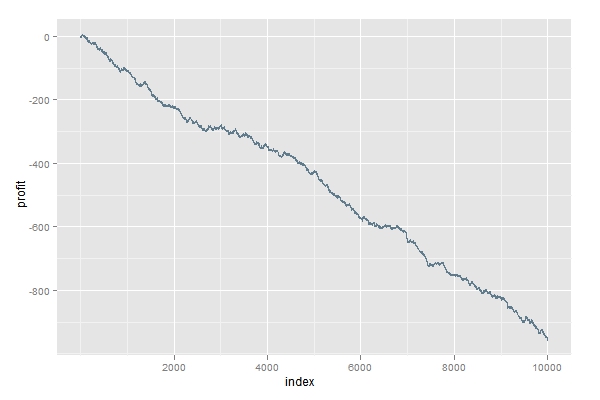
好了，前面铺垫了这么多，那么下面我们用R语言来验证一下21点的赚钱方法。首先编写了抽牌函数card.select和玩21点的函数game（代码写得有点糙，如果你有更好的想法请告诉我）。先考查一种情景，如果大牌比例较低而且我们采取和庄家一样的策略，即在16点以下继续要牌，经过一万次模拟后发现会大输特输。原因就在于：当玩家先爆牌时，庄家自然获胜。经计算这一规定的优势相当大。下图即此情景下的积累收益图，真是银河落九天啊。

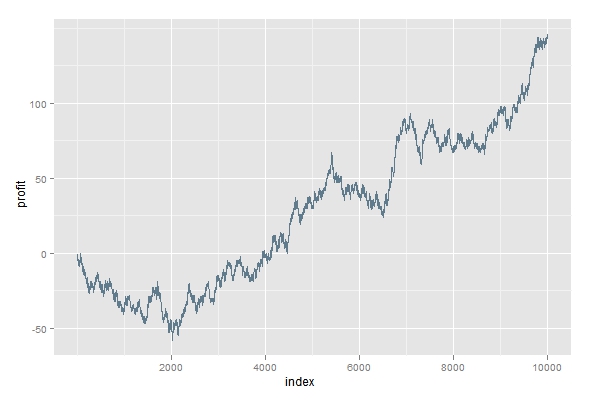
再看第二次情景，当我们将card.select中的m参数默认值改为6，此时大牌与小牌的比例约为2.5：1。然后将玩家player的判断阀值设为12，再进行模拟一万次。从下图会发现玩家的累积收益在起初会有负值，之后较为稳定的增长。一万次游戏后大约赚取了150元（假设每次下注1元）。从二项检验的结果也可以看到，p值为0.06较小，而胜率的估计区间为0.499到0.525。由此可见，等待大牌的确可以增加玩家的胜算。

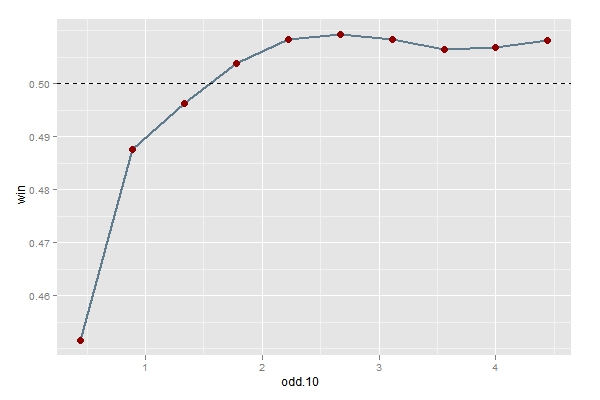
为了仔细考查大小牌之比和胜率之间的关系，我们再重复模拟多次，得到下图。横轴为大牌与小牌之间的比率，纵轴为玩家的胜负比率。可以观察到当大小牌之比达到1.5：1时，玩家的胜率即可超过50%。

你可能会为此而雀跃，恨不得马上飞到澳门去试一把。但是你要注意的是：如果一把牌玩一分钟，一万次游戏需要你不吃不喝不睡连续七天时间，而七天时间你才赚了150元。而且这种大牌比率极高的情况是少见的，你也许要侦查多个牌桌才会得到机会。而且我们的模拟也没有考虑到其它的情况：如多人桌、分牌、保险等因素。也没有考虑到玩家的资金使用策略。最重要的是：赌场会洗牌！重新洗牌之后，条件概率就不复存在，而在此基础上的算牌法所获得的胜率也不再有效。

R代码如下：

# 从13张扑克牌中抽一张牌的函数，用n和m来控制大小牌的抽取概率
card.select <- function(n=1,m=6) {
 x <- sample(1:13,1,prob=rep(c(n,m),c(9,4))/sum(rep(c(n,m),c(9,4))))
 # J，Q，K都被转为10点
 x <- ifelse(x>10,10,x)
 return(x)
}
 
# 完成一次二十一点游戏的函数，point为是否继续要牌的判断阀值
game <- function(point) {
  # 最开始得到的两张牌
  select <- c(card.select(),card.select())
  # 将原始序列select中的1点转成11点，求牌的点数和
  Ato11 <- select
  Ato11[Ato11==1] <- 11
  card.sum <- sum(Ato11)
  # 进入条件循环，以判断是否应该继续要牌
  #若牌点数和大于阀值，则不再要牌
  while (card.sum <= point) { 
    select <- c(select, card.select())
    Ato11 <- select
    Ato11[Ato11==1] <- 11
    card.sum <- sum(Ato11)
 }  
  # 若点数和大于21且其中有A，则A看作1点，用原始的序列求和
  if (card.sum > 21 && 1 %in% select) {
  card.sum <- sum(select)
  }
  # A转为1点后，再次条件循环，以判断是否应该继续拿牌
  while (card.sum <= point) {
    select <- c(select, card.select())
    card.sum <- sum(select)
 }
  # 若点数大于21点，则爆牌为0  
  y <-ifelse((card.sum<=21),card.sum,0)
 return(y)
# cat('select=',select,'\n','return=',y,'\n')
}
 
# 与庄家博弈，赌场规定庄家以16为阀值，玩家应以12为阀值，等待庄家爆掉
player <- replicate(100000,game(12))
dealer <- replicate(100000,game(16))
#结果有赢输平三种情况
result <-ifelse(player > dealer,1,ifelse(player < dealer,-1,0))
# 若二者均爆牌且平局，设玩家输
result[player==0 & result==0] <- -1
# 将平的情况略去以方便进行二项检验
result.no.tie <- result[result!=0]
# 二项检验
binom.test(length(result.no.tie[result.no.tie==1]),length(result.no.tie))
# 观察玩家连赢或连输的游程
table(rle(result))
# 计算累积利润
profit <- cumsum(result)
# 绘图以观察利润变化
q <- ggplot(data.frame(profit,index=1:length(profit)),aes(index,profit))
q + geom_line(colour='lightskyblue4')
 
# 考查在不同的大小牌比值的情况下，玩家获胜的概率
odd.10 <-  win <- rep(0,10)
for (i in 1:10) {
    card.select <- function(n=1,m=i) {
        x <- sample(1:13,1,prob=rep(c(n,m),c(9,4))/sum(rep(c(n,m),c(9,4))))
        x <- ifelse(x>10,10,x)
        return(x)
    }
    odd.10[i] <- 4*i/9 
    player <- replicate(100000,game(12))
    dealer <- replicate(100000,game(16))
    result <-ifelse(player > dealer,1,ifelse(player < dealer,-1,0))
    result[player==0 & result==0] <- -1
    result.no.tie <- result[result!=0]
    win[i] <- length(result.no.tie[result.no.tie==1])/length(result.no.tie)
}
 
d <- ggplot(data.frame(odd.10,win),aes(odd.10,win))
d + geom_line(colour='lightskyblue4',size=1) + 
    geom_point(colour='red4',size=3.5) +
    geom_hline(y=0.5,linetype=2)