用glmnet包实施套索算法(LASSO)

当我们使用数据训练分类器的时候，很重要的一点就是要在过度拟合与拟合不足之间达成一个平衡。防止过度拟合的一种方法就是对模型的复杂度进行约束。模型中用到解释变量的个数是模型复杂度的一种体现。控制解释变量个数有很多方法，例如变量选择(feature selection)，即用filter或wrapper方法提取解释变量的最佳子集。或是进行变量构造(feature construction)，即将原始变量进行某种映射或转换，如主成分方法和因子分析。变量选择的方法是比较“硬”的方法，变量要么进入模型，要么不进入模型，只有0-1两种选择。但也有“软”的方法，也就是Regularization类方法，例如岭回归(Ridge Regression)和套索方法(LASSO:least absolute shrinkage and selection operator)。

这两种方法的共同点在于，将解释变量的系数加入到Cost Function中，并对其进行最小化，本质上是对过多的参数实施了惩罚。而两种方法的区别在于惩罚函数不同。但这种微小的区别却使LASSO有很多优良的特质（可以同时选择和缩减参数）。下面的公式就是在线性模型中两种方法所对应的目标函数：

公式中的lambda是重要的设置参数，它控制了惩罚的严厉程度，如果设置得过大，那么最后的模型参数均将趋于0，形成拟合不足。如果设置得过小，又会形成拟合过度。所以lambda的取值一般需要通过交叉检验来确定。

在R语言中可以使用glmnet包来实施套索算法。我们采用的数据集是Machine Learning公开课中第七课的一个算例。先来看看这个样本数据的散点图。下图显示有两个类别等待我们来区分。显然其决策边界是非线性的，所以如果要用Logistic Regression来作分类器的话，解释变量需要是多项式形式。但这里存在一个问题，我们应该用几阶的多项式呢？如果阶数过高，模型变量过多，会存在过度拟合，而反之阶数过少，又会存在拟合不足。所以这里我们用LASSO方法来建立Logistic回归分类器。

分析步骤如下：

• 根据算例要求，先生成有六阶多项式的自变量，这样一共有28个自变量；
• 用glmnet包中的cv.glmnet函数建模，该函数自带交叉检验功能；
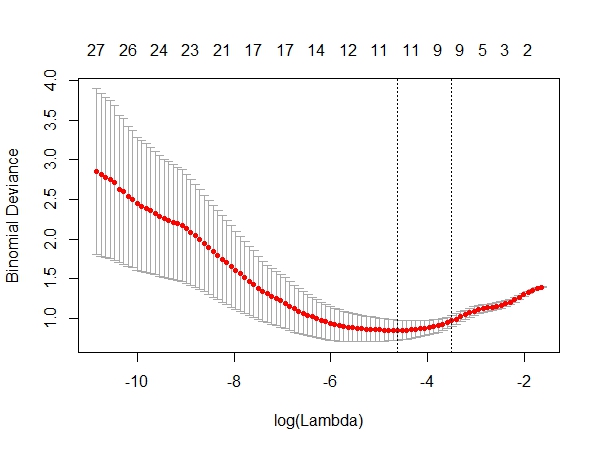
• 根据上面的结果绘制CV图如下，从中选择最佳lambda值。

cv.glmnet函数利用交叉检验，分别用不同的lambda值来观察模型误差。上图横轴是lambda值的对数，纵轴是模型误差。从上面的图可以看到，最佳的lambda取值就是在红色曲线的最低点处，对应着变量个数是11个。它右侧的另一条虚线是在其一倍SE内的更简洁的模型（变量个数为9）。由于这两个lambda对应的模型误差变化不大，而我们更偏好于简洁的模型，选择对应的lambda值为0.025。

在使用cv.glmnet函数选择lambda值之后，我们没有必要去运行glmnet函数，直接从结果中就可以提取最终模型（9个变量）并获得参数系数。为了利于比较我们还提取了原始模型（28个变量）的参数系数。

最后我们要在原来的散点图上画出两条决策边界，一条是根据LASSO方法得到的9变量模型，下图中紫色曲线即是它决策边界，决策边界比较平滑，具备很好的泛化能力。另一条是28个变量的原始模型。 蓝色曲线即是它的决策边界，它为了拟合个别样本，显得凸凹不平。

如果你的数据变异较大，那么在做LASSO之前最好进行数据标准化处理。LASSO的进一步扩展是和岭回归相结合，形成Elastic Net方法。glmnet包也可以实施这种算法。

参考资料：
《The Elements of Statistical Learning》
《Machine Learning for Hackers》
http://www-stat.stanford.edu/~tibs/lasso.html
http://datamining.dongguk.ac.kr/ftp/temp/Regularization.pdf
http://ygc.name/2011/10/26/machine-learning-5-2-regularized-logistic-regression/

本例的R代码在此。