一个简单的狼兔追逐问题

四月八日，也就是春分月圆之后的首个星期日即是复活节(Easter)。而复活节兔是复活节象征之一。作为多产动物的兔子，象征了春天的复苏和新生命的诞生。此外，兔子是爱神阿弗洛狄特的宠物，也是日耳曼土地女神霍尔塔的持烛引路者。今天我们就来谈一个关于兔子的问题。狼兔追逐问题是欧洲文艺复兴时代达芬奇提出的一个数学问题。题目描述如下：一只兔子在O点外，其洞穴在正北20米的B处，一只狼位于兔子正东33米的A处。当两只动物同时发现对方以后，兔子奔向自己的洞穴，狼以快于兔子一倍的速度紧追兔子不放。狼在追赶过程中所形成的轨迹就是追击曲线。狼是否会在兔子跑回洞穴之前追赶上兔子？

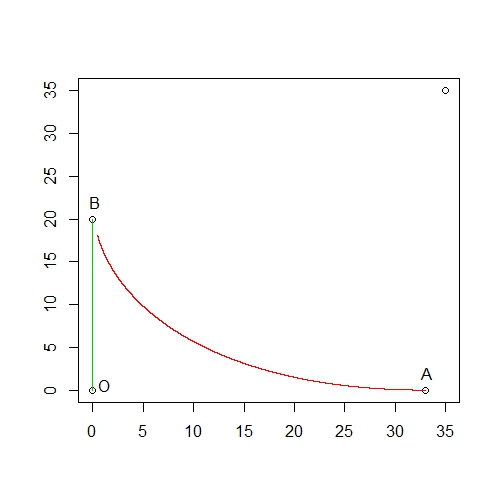
这个问题也是《统计模拟及其R实现》一书后面的一个习题。我们先建立一个函数，参数为二者运动速度之比v，一个微小的位移delta_T，以及狼可以捕获兔子的最短距离eps。基本思路是先画出初始位置，然后用两个矩阵来存放二者的坐标。然后利用一个for循环来不断更新坐标数据。d为二者之间的距离，如果在循环结束时，d小于eps则意味着狼抓住了兔子，否则就是失败。函数会画出追击曲线，并根据情况返回逻辑值。如果抓住返回真值，并获得抓住点坐标。如果失败返回假值，并获得二者最后的距离。实际从结果来看，狼未能在兔子跑回洞穴之前追赶上兔子。但你可以试着将v值设置的大一些，大约在2.3左右，狼就可以成功追上兔子了。

R代码如下：

# V为狼与兔子的运动速度之比，delta_T为瞬间移动
# eps为可以抓到的距离
trace <- function(v=2,delta_T=0.001,eps=0.01) {
  plot(c(0,33,35,0),c(0,0,35,20),xlab='',ylab='')
  text(0,20,labels='B',adj=c(0.3,-0.8))
  text(33,0,labels='A',adj=c(0.3,-0.8))
  text(0,0,labels='O',adj=c(-0.5,0.1))
  # x为兔子的坐标矩阵，y为狼的坐标矩阵
  x <- matrix(c(0,0),nrow=1)
  y <- matrix(c(33,0),nrow=1)
  a <- 0
  b <- 0
  time <- 20/delta_T
  for (j in 1:time) { 
    # d为二者之间的距离，a为兔子的新位置，b为狼的新位置
    d <- sqrt((x[j,1]-y[j,1])^2+(x[j,2]-y[j,2])^2)
    a[1] <- 0
    a[2] <- x[j,2] + delta_T
    b[1] <- y[j,1] + v*delta_T*(x[j,1] - y[j,1])/d
    b[2] <- y[j,2] + v*delta_T*(x[j,2] - y[j,2])/d
    # 若距离小于抓捕距离则离开循环
    if(d < eps) break
    # 将新位置加入到坐标矩阵中
    x <- rbind(x,a)
    y <- rbind(y,b)
  }
  # 绘制二者的追逐路线
  lines(x[1:j,1],x[1:j,2],col=3)
  lines(y[1:j,1],y[1:j,2],col=2)
  if ( d < eps & j <= time) return(list(result='TRUE',x=x[[j,1]],y=x[[j,2]]))
  else return(list(result='FALSE',dist=as.vector(d)))
}
trace()