当时搭乘泰坦尼克号的乘客都留下了详细的资料,本文试图利用这个资料来建立各种图表,以回答这样一个问题:在当时什么样的人存活率最高?涉及的数据集中包括了四个变量:是否获救Survived,所在舱Class,年龄Age,性别Sex。我们首先从网络上读取数据文件,进行简单的统计描述。
| Class | Age | Sex | Survived |
| Crew:885 | Adult:2092 | Female:470 | No:1490 |
| First:325 | Child:109 | Male:1731 | Yes:711 |
| Second:285 Third:706 |
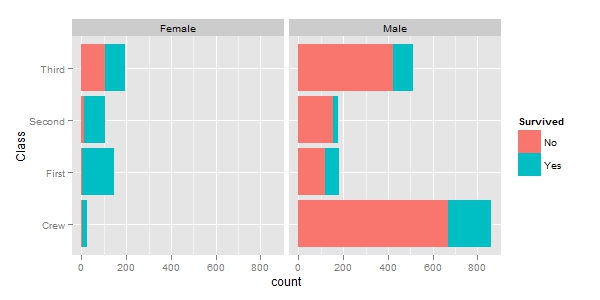
从上面的结果可以看到,三等舱和船员所占人数较多,儿童人数很少,女性和男性比例大约为1:3.5,整体存活率在30%左右。下一步我们用ggplot2包绘制条形图,以观察性别和所在舱对存活的影响。从下图可以看到,就整体而言女性的存活率高于男性。这一点证实了当时“让妇女和孩子先走”的援救原则。如果将舱位因素考虑进来。一、二等舱的女性存活率都相当高,在船员中的少量女性也得以存活,但是三等舱的女性相对而言存活率较低。因此,虽然同为女性,但舱位的差别仍然决定了生死的命运。
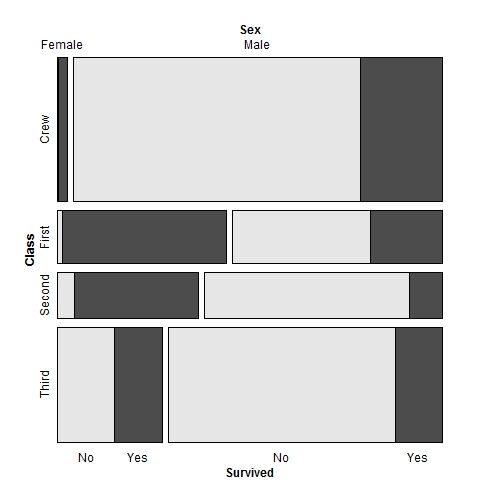
我们还可以用马赛克图来表现各分类变量的影响。下图中不同的矩形代表了不同的群体人数,每个矩形又根据是否存活划分为黑白两个部分。从中还可以观察到一些有趣结论,例如男性船员的存活率低于三等舱的女性,但在绝对值上则占优。
为了精确的得到各个群体的存活率,我们将原始数据汇总得到下表。观察到存活率最高的是一、二等舱的儿童。但同时也看到三等舱的儿童存活率则低于50%。其中的原因值得我们思考。存活率居次的是女性,但三等舱的女性存活率几乎只有二等舱的一半。这同样说明了地位的差别。存活率居后的是男性群体,但一等舱的男性存活率仍相对较高,最惨的则是二等舱的男性,只有8%的存活率。
| 级别 | 性别 | 年龄 | 人数 | 获救数 | 存活率 |
| First | Female | Child | 1 | 1 | 100.00% |
| Second | Female | Child | 13 | 13 | 100.00% |
| First | Male | Child | 5 | 5 | 100.00% |
| Second | Male | Child | 11 | 11 | 100.00% |
| First | Female | Adult | 144 | 140 | 97.00% |
| Crew | Female | Adult | 23 | 20 | 87.00% |
| Second | Female | Adult | 93 | 80 | 86.00% |
| Third | Female | Adult | 165 | 76 | 46.00% |
| Third | Female | Child | 31 | 14 | 45.00% |
| First | Male | Adult | 175 | 57 | 33.00% |
| Third | Male | Child | 48 | 13 | 27.00% |
| Crew | Male | Adult | 862 | 192 | 22.00% |
| Third | Male | Adult | 462 | 75 | 16.00% |
| Second | Male | Adult | 168 | 14 | 8.00% |
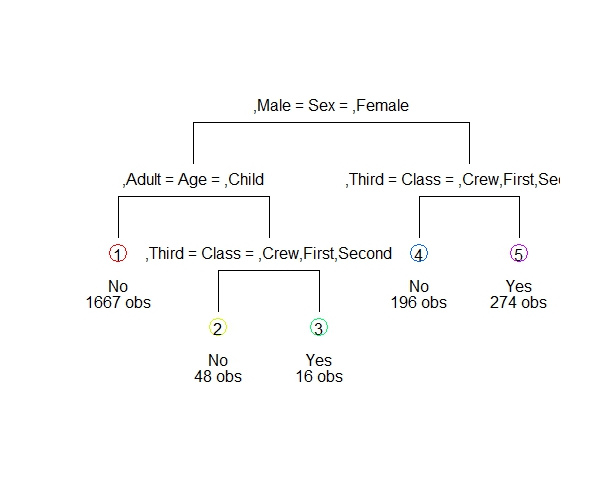
下面我们用决策树模型来观察哪个因素对存活率最为重要。决策树将根据最重要的变量将数据进行划分,从下图看到“性别”是最重要的影响因素,如果你是女性,那么决定存活的因素为舱位,如果你是男性,那么决定存活的因素变为年龄。
结论:如果你不幸穿越到了100年前的Titanic上,你应该变身为女性或小正太,同时藏身于一等舱中,这样你的存活率会大大的提升。从上面的图表可以了解到,妇女和孩子的确得到了一定的优先援救,但舱位也是决定存活率的重要因素。为什么三等舱的存活率低?这是因为船舱裂口在三等舱吗?还是什么其它原因,这就留待各位挖掘了。
R代码:
# 获取数据
url <- 'http://stats.math.uni-augsburg.de/Mondrian/Data/Titanic.txt'
data <- read.table(url,T)
summary(data)
# 绘制条形图
library(ggplot2)
p <- ggplot(data,aes(x=Class,fill=Survived))
p + geom_bar(position='stack')+ coord_flip() + facet_wrap(~Sex)
# 绘制mosaic图
library(vcd)
mosaic(Survived~ Class+Sex, data = data,shade=T, highlighting_direction = "right")
# 建立存活率表
fx <- function(x) length(x[x=='Yes'])
table1 <- data.frame(with(data,aggregate(x=Survived,by=list(Class,Sex,Age),FUN=length)))
table2 <- data.frame(with(data,aggregate(x=Survived,by=list(Class,Sex,Age),FUN=fx)))
table1$y <- table2$x
table1$survived <- round(table1$y /table1$x,digits=2)
table1[order(table1$survived,decreasing=T),]
# 建立决策树模型
library(rpart)
formula <- Survived~ Class+Sex+Age
fit <- rpart(formula,data)
library(maptree)
draw.tree(fit)
参考资料:生活中的统计学--从铁达尼号沉船资料谈起

感觉用 log-linear model 也可以吧。
回复删除对数-线性模型?自变量可都是分类数据啊。而且决策树对于数据不需要什么假设。
删除对的,就是 GLM 里面对 contingency table 的分析。
删除好巧啊,今天刚交过这个数据分析的作业,用的是logistics regression,不过还是很多地方不太明白。。。
回复删除很多学校都拿这个数据集开刀示范的。
删除