R语言多元分析系列之四：判别分析

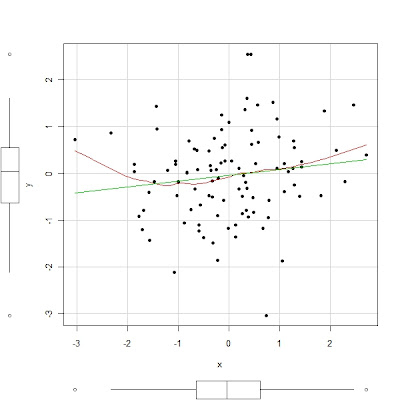
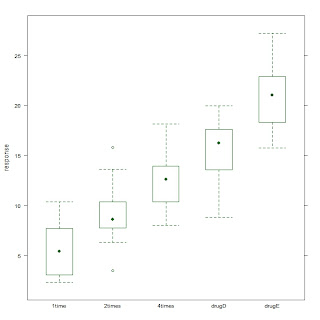
判别分析（discriminant analysis）是一种分类技术。它通过一个已知类别的“训练样本”来建立判别准则，并通过预测变量来为未知类别的数据进行分类。

判别分析的方法大体上有三类，即Fisher判别、Bayes判别和距离判别。Fisher判别思想是投影降维，使多维问题简化为一维问题来处理。选择一个适当的投影轴,使所有的样品点都投影到这个轴上得到一个投影值。对这个投影轴的方向的要求是：使每一组内的投影值所形成的组内离差尽可能小，而不同组间的投影值所形成的类间离差尽可能大。Bayes判别思想是根据先验概率求出后验概率，并依据后验概率分布作出统计推断。距离判别思想是根据已知分类的数据计算各类别的重心，对未知分类的数据，计算它与各类重心的距离，与某个重心距离最近则归于该类。

R语言多元分析系列之三：多维标度分析

多维标度分析(MDS)是一种将多维空间的研究对象简化到低维空间进行定位、分析和归类，同时又保留对象间原始关系的数据分析方法。

设想一下如果我们在欧氏空间中已知一些点的座标，由此可以求出欧氏距离。那么反过来，已知距离应该也能得到这些点之间的关系。这种距离可以是古典的欧氏距离，也可以是广义上的“距离”。MDS就是在尽量保持这种高维度“距离”的同时，将数据在低维度上展现出来。从这种意义上来讲，主成分分析也是多维标度分析的一个特例。

R语言多元分析系列之二：探索性因子分析

探索性因子分析（Exploratory Factor Analysis，EFA）是一项用来找出多元观测变量的本质结构、并进行处理降维的技术。 因而EFA能够将具有错综复杂关系的变量综合为少数几个核心因子。EFA和PCA的区别在于：PCA中的主成分是原始变量的线性组合，而EFA中的原始变量是公共因子的线性组合，因子是影响变量的潜在变量，变量中不能被因子所解释的部分称为误差，因子和误差均不能直接观察到。进行EFA需要大量的样本，一般经验认为如何估计因子的数目为N，则需要有5N到10N的样本数目。

虽然EFA和PCA有本质上的区别，但在分析流程上有相似之处。下面我们用ability.cov这个心理测量数据举例，其变量是对人的六种能力，例如阅读和拼写能力进行了测验，其数据是一个协方差矩阵而非原始数据。R语言中stats包中的factanal函数可以完成这项工作，但这里我们使用更为灵活的psych包。

R语言多元分析系列之一：主成分分析

主成分分析（principal components analysis， PCA）是一种分析、简化数据集的技术。它把原始数据变换到一个新的坐标系统中，使得任何数据投影的第一大方差在第一个坐标（称为第一主成分）上，第二大方差在第二个坐标（第二主成分）上，依次类推。主成分分析经常用减少数据集的维数，同时保持数据集的对方差贡献最大的特征。这是通过保留低阶主成分，忽略高阶主成分做到的。这样低阶成分往往能够保留住数据的最重要方面。但是在处理观测数目小于变量数目时无法发挥作用，例如基因数据。

R语言中进行主成分分析可以采用基本的princomp函数，将结果输入到summary和plot函数中可分别得到分析结果和碎石图。但psych扩展包更具灵活性。

新书推荐：《Visualize This》

这是一个数据的时代，各种数据铺天盖地涌现出来，如何从中获取有用的信息？人类的大脑喜欢图形，因此将数据可视化或许是种方法。数据可视化是美学、数据分析和专业知识的结合，能以清晰简明而优美的方式讲述数据背后的故事。

如果你对数据可视化感兴趣，那么向你推荐Visualize This这本书。作者Nathan Yau是加州大学洛杉矶分校统计学博士生。同是也是flowingdata.com的创建者。

缺失数据的处理

对于缺失数据通常有几种应付手段，一种是当缺失数据较少时直接删除相应样本，另一种是对缺失数据进行插补，最后是使用对缺失数据不敏感的分析方法，例如决策树。基本上缺失数据处理的流程是首先判断其模式是否随机，然后找出缺失的原因，最后对缺失值进行处理。

qplot绘图函数快速入门

绘图是进行数据探索分析的重要方法，也是数据报告中的必备元素。但进行多元数据绘图时，R语言中的基本绘图工具往往很不给力，使用lattice包又要记一大堆命令。在你痛苦不堪的时候，需要ggplot2包来拯救你。虽然在刚开始学习这种绘图方法时会有少许难度，但跨过这道坎后你会感觉到它的简洁和力量。

对于初学者ggplot2提供了qplot函数，可以方便的绘制多种图形，下面来看看它是如何作的。首先加载ggplot2包，然后读取diamonds数据，运行?diamonds可以得到关于数据的更多信息。由于该数据集非常大，所以为了举例方便从中抽取了500个样本。

多层回归模型简介

多层回归模型（Multi-level model）中有很多容易混淆的概念，因为很多概念是来源于不同的专业背景。首先让我们先罗列这些名词进行区分，再来R语言来举例。

多层回归模型通常涉及到对同一个体进行反复测量，这样得到的数据就不再相互独立而是存在某种相关性，所以普通线性回归不再适用。当这种反复测量是在不同时点上进行时，这就称为面板数据分析（panel data analysis）或者纵向数据分析（longitudinal data analysis）。

加性模型（Additive Model）在R中的实现

加性模型是一种非参数模型，如果说二维散点图的平滑是简单线性回归模型的一般化，那么加性模型就是多元回归模型的一般化。加性模型非常具有灵活性，因为它不象参数模型那样需要假设某种函数形式，只要预测变量对响应变量的影响是独立即可，也称为可加和假设。

加性模型的拟合是通过一个迭代过程（向后拟合算法）对每个预测变量进行样条平滑。其算法要在拟合误差和自由度之间进行权衡最终达到最优。在R中可以利用mgcv包中的gam函数实现加性模型，我们仍以trees数据集作为例子，其中Volume为响应变量，Girth和Height为预测变量。

在R语言中进行局部多项式回归拟合（LOESS）

局部多项式回归拟合是对两维散点图进行平滑的常用方法，它结合了传统线性回归的简洁性和非线性回归的灵活性。当要估计某个响应变量值时，先从其预测变量附近取一个数据子集，然后对该子集进行线性回归或二次回归，回归时采用加权最小二乘法，即越靠近估计点的值其权重越大，最后利用得到的局部回归模型来估计响应变量的值。用这种方法进行逐点运算得到整条拟合曲线。

在R语言中进行局部多项式回归拟合是利用loess函数，我们以cars数据集做为例子来看下使用方法。该数据中speed表示行驶速度，dist表示刹车距离。用loess来建立模型时重要的两个参数是span和degree，span表示数据子集的获取范围，取值越大则数据子集越多，曲线越为平滑。degree表示局部回归中的阶数，1表示线性回归，2表示二次回归，也可以取0，此时曲线退化为简单移动平均线。这里我们设span取0.4和0.8，从下图可见取值0.8的蓝色线条较为平滑。

在R语言中用自助法求统计量置信区间

当样本不符合理论分布假设时，求样本统计量的置信区间就成为一个难题。而自助法(Bootstrap)的思路是对原始样本重复抽样产生多个新样本，针对每个样本求取统计量，然后得到它的经验分布，再通过求经验分布的分位数来得到统计量的置信区间，这种方法不需要对统计量有任何理论分布的假设。一般认为，只要样本具有代表性，采用自助法需要的原始样本只要20-30个,重复抽样1000次就能达到满意的结果。

在R中进行自助法是利用boot扩展包，其流程如下：

参数检验、非参数检验与置换检验的比较

当我们研究的样本处于良好情况下（近似正态、无离群点、数据量大等），传统的参数检验是很有效的。但是当这些前提条件不再满足时，参数检验就不再有效。此时人们往往求助于非参数检验，非参数检验不再关注数据的值，而只关注数据的秩，这样就抛弃了大量可用的信息。而置换检验采取重复随机抽样的方法，通过对样本再抽样构造经验分布，然后在此基础上生成P值进行推断，达到很好的效果。但要注意的是，如果样本不能很好的代表总体，任何检验方法都是无效的。

聊聊散点图

散点图很简单，但它无疑是探索数值数据之间关系的有力工具。它有直观简便的优点，通过观察散点图，不但可以得到定性的结论，而且可以通过观察并处理异常数据，提高用于估算相关程度的准确性。在R中实现散点图最简单的函数就是plot，我们首先随机生成两个数据，然后用作散点图

y=rnorm(100)
x=rnorm(100)
plot(x,y)

如果希望从简单的散点图中得到更多信息，我们可以使用car包中的scatterplot函数，散点图增加了单变量的箱线图，线性回归线和局部回归线。此外该函数也可以进行条件绘图。

scatterplot(x,y,spread=F)

R语言中的方差分析

1 单因子方差分析（one-way ANOVA）
1)建模：
我们采用multcomp包中的cholesterol数据集作为例子，其中response为响应变量，trt为预测变量，这个处理中有五种水平。从下面的箱形图中可观察到处理的不同水平对于响应变量的影响。再用aov函数建立单因子方差模型，从结果的P值可看到各组均值有显著不同。

aggregate(response, by=list(trt), FUN=mean)
bwplot(response~trt)
model=aov(response~trt)
summary(model)