R语言中的方差分析

1 单因子方差分析（one-way ANOVA）
1)建模：
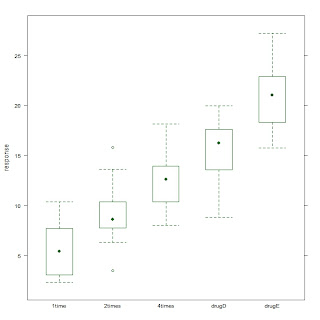
我们采用multcomp包中的cholesterol数据集作为例子，其中response为响应变量，trt为预测变量，这个处理中有五种水平。从下面的箱形图中可观察到处理的不同水平对于响应变量的影响。再用aov函数建立单因子方差模型，从结果的P值可看到各组均值有显著不同。

aggregate(response, by=list(trt), FUN=mean)
bwplot(response~trt)
model=aov(response~trt)
summary(model)

2)多重比较：
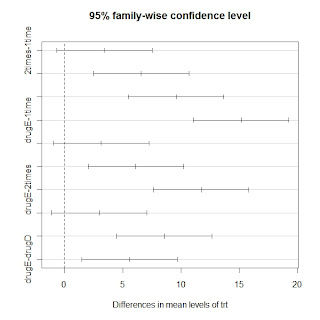
方差分析只告诉我们这五组之间是不同的，但没有告诉我们哪两组之间有明显差别，此时需要使用TukeyHSD函数进行均值的多重比较分析，从结果中观察到有三个两两比较是不显著的。

(result=TukeyHSD(model))
plot(result)

3)假设检验：
方差分析需要一定的假设，即数据集应该符合正态和同方差，我们分别用下面的函数来进行检验，从P值观察到这两个假设是符合的。对于不符合假设的情况，我们就要用到非参数方法，例如Kruskal-Wallis秩和检验

shapiro.test(response)
bartlett.test(response~trt)

2 双因子方差分析（Two-way Factorial ANOVA）
我们用ToothGrowth数据集来举例双因子方差分析。其中supp和dose是预测变量，len是响应变量。我们仍然使用aov进行建模，然后使用HH包的绘图函数来展现双因子交互效果图

fit <- aov(len ~ supp*dose)
library(HH)
interaction2wt(len~supp*dose)

要注意在下面的情况下因子的先后顺序是有讲究的：

• 第一种情况是多因子非平衡情况下，此时重要的因子应该放在前面，
• 第二是在在有协变量情况下，此时协变量放在前面，然后是主因子和交互因子

3 重复测量方差分析
在重复测量的方差分析中，实验对象被测量多次，所以会存在组内因子，组内因子要以下面的形式特别标明出来，其中B是组间因子，W是组内因子，subject是实验对象的ID，

model=aov(Y ~ B * W + Error(Subject/W))

上述方法的前提是对应组内因子不同水平的数据是等方差的，当传统方法的假设得不到满足时，则应用lme4包中lmer函数，利用混合效应模型来解决问题。