利用optim最优化函数进行曲线拟合

R语言中对函数求极值有两种命令，较简单的是optimize函数，在确定搜索范围后可对一元函数求极值，例如：

f = function(x) 3*x^4 − 2*x^3 + 3*x^2 − 4*x + 5
optimize(f, lower=-20, upper=20)
$minimum
[1] 0.5972778
$objective
[1] 3.636756

在对多元函数求极值时，则需利用到更强大的optim函数，本例来自于《Introduction to Scientific Programming and Simulation Using R》，其中数据可从spuRs包中获得。本例的目标是对树木体积进行建模，自变量为树龄，函数形式为指数形式，其中包括了三个待定参数。

首先建立模型函数

richards = function(t, theta){
theta[1]*(1 - exp(-theta[2]*t))^theta[3]}

再利用最小二乘建立误差函数

 loss = function(theta, age, vol){
 sum((vol - richards(age, theta))^2)}

读入数据

 trees = read.table('clipboard',T)
 tree = trees[trees$ID=="1.3.11", 2:3]

确定搜寻参数起始点

 theta0 <- c(1000, 0.1, 3)

求使误差最小化的参数值，optim命令中第一项为起始点，第二项为目标函数，后面的是所需数据变量，optim命令的默认方法是Nelder-Mead算法，它是求多维函数极值的一种算法，由Nelder和Mead提出，又叫单纯形算法，但和线性规划中的单纯形算法是不同的，由于未利用任何求导运算，算法比较简单，但收敛速度较慢，适合变量数不是很多的方程求极值

 theta.L <- optim(theta0, loss, age=tree$Age, vol=tree$Vol)

绘制拟合图形

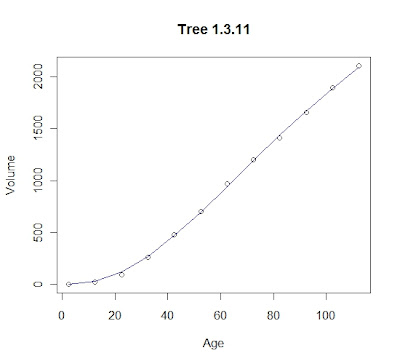
 plot(tree$Age, tree$Vol, xlab="Age", ylab="Volume", main='Tree 1.3.11')
 lines(tree$Age, richards(tree$Age, theta.L$par), col="blue")

观察拟合结果，若convergence取0则表明收敛成功，可以看到本例的最小误差为2773，而par则是三个最佳参数。

theta.L2
$convergence
[1] 0
$par
[1] 3.596401e+03 1.541453e-02 2.779727e+00
$value
[1] 2773.842